BCD 09.04.2023 (Easter Sunday edition)

If, unlike me, you’ve ever wondered what day Easter Sunday will fall on in some given year, you could look at a calendar. Or you could ask Google.

Or you could quickly work it out for yourself using this simple calculation for our bonehead calculation of the day (BCD):

1. Divide x (= the desired year of the Gregorian calendar) by 19 to get a quotient (which we ignore) and a remainder A. This is the year’s position in the 19-year lunar cycle. (A + 1 is the year’s golden number.)
2. Divide x by 100 to get a quotient B and a remainder C.
3. Divide B by 4 to get a quotient D and a remainder E.
4. Divide 8B + 13 by 25 to get a quotient G and a remainder (which we ignore).
5. Divide 19A + B – D – G + 15 by 30 to get a quotient (which we ignore) and a remainder H. (The year’s epact is 23 – H when H is less than 24 and 53 – H otherwise.) 
6. Divide A + 11H by 319 to get a quotient M and a remainder (which we ignore).
7. Divide C by 4 to get a quotient J and a remainder K.
8. Divide 2E + 2J – K – H + M + 32 by 7 to get a quotient (which we ignore) and a remainder L.
9. Divide H – M + L + 90 by 25 to get a quotient N and a remainder (which we ignore).
10. Divide H – M + L + N + 19 by 32 to get a quotient (which we ignore) and a remainder P. Easter Sunday is the Pth day of the Nth month (N can be either 3 for March or 4 for April). The year’s dominical letter can be found by dividing 2E + 2J – K by 7 and taking the remainder. A remainder of 0 is equivalent to the letter A, 1 is equivalent to B, and so on).

(The following figure is the same thing, I think, or at least does the same thing, just for the more visually inclined.)

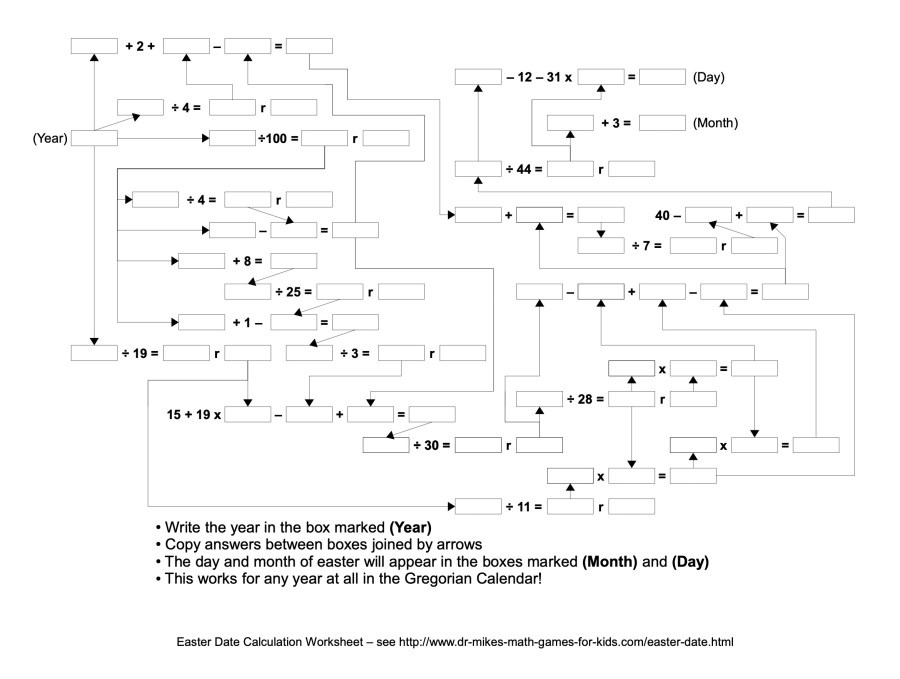
Really??? Who came up with this? And how?!

Wouldn’t just choosing some date and running with it, say maybe two days after the date that most scholars agree that Jesus was crucified, be simpler?